 |
Въведение във фракталния анализ на природни структури
Цв. Георгиев*,1
1 Нов Български Университет, департамент „Науки за Земята и околната среда” ул. Монтевидео 21, София 1618, България
материала в PDF
An introduction to the fractal analysis of natural structures
Ts. Georgiev1
1 New Bulgarian University, Department of Earth and Environmental Sciences, 1618 Sofia, 21 Montevideo str. Bulgaria
Key words fractals, fractal plots, fractal dimensions
The fractals concept, chaqracterizing the apparent chaos of various natural structures, is presented and commented. The characteristics fractal slope and fractal dimension are introduced on the base of known mathematic fractals. The fundamental plots in log-log coordinates such as “step size – object size” for curves, surfaces and bodies, as well as “area of the object – perimeter of the object”, for planar curves are regarded. The describing is accompanied with examples and illustrations. A special mathematic fractal, named “Jagged cloud”, is generated for elucidation of the sense of the fractallity in the context of the perimeter – area relation. Classic examples about the fractallity of the lengths of coast and land frontiers, atmosphere clouds, solar granules, fracture surfaces etc., are given.
1. Самоподобност и фракталност при повърхности и профили
Когато метален детайл се счупи поради опън, натиск или удар, фрактурната повърхност е грапава (нерегулярна, назъбена), защото в металната микроструктура присъстват гранули, домени и примеси. При разглеждане на повърхността с увеличаваща се разделителност се разкриват множество по-фини назъбени структури (фиг.1). При това наблюдателят не вижда детайли с характерни размери, но чувства някаква самоподобност на грапавостта на различни мащаби. Така е и при други фрактурни повърхности, например при счупени кост или дърво, където назъбеността е много по-силно изразена.
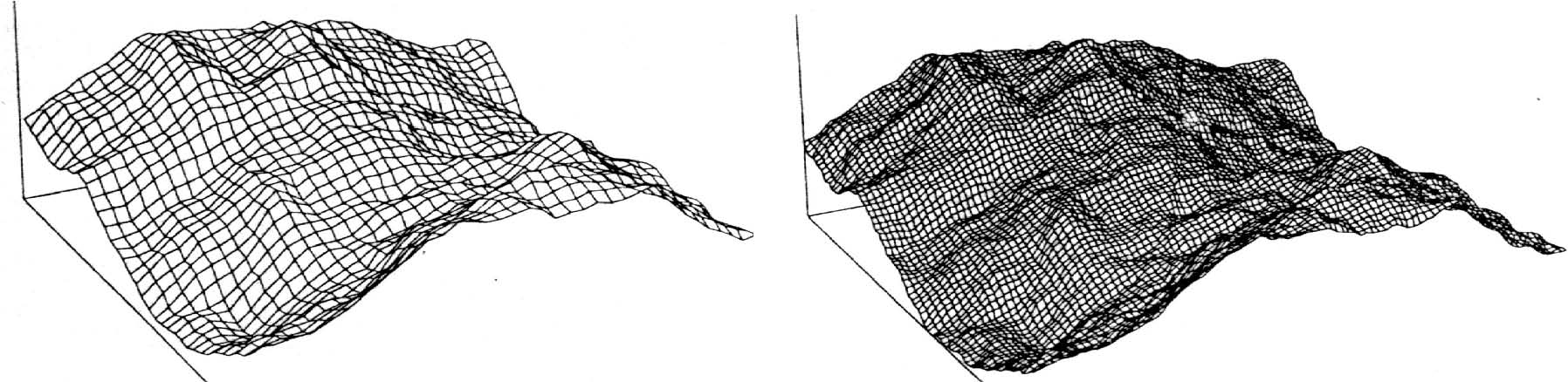
Фиг. 1. Класически пример за фрактал – фрактурна повърхност, представена с по-малка (вляво) и по-голяма (вдясно) разделителност. Във втория случай се виждат повече и по-дребни детайли [1].
* Corresponding author: e-mail tsgeorgiev@nbu.bg
Различни природни структури, както и специално генерирани математически обекти се характеризират със самоподобна на различни мащаби грапавост или фрагментарност. Такава самоподобност в привидния хаос, която е еквивалентна на отсъствие на детайли с характерни размери и не се подава на количествено изследване с обичайни методи, се нарича фракталност, а структурата, притежаваща това качество – фрактал.
Понятията самоподобност и фракталност, заедно с обща геометрична теория, методи и приложения, са довъведени в науката на базата на примера с фрактурната повърхност в монографията-есе на Беноа Манделброт „The Fractal Geometry of the Nature” [1]. Множество методи за анализ на природни фрактални структури са събрани монографиите на Джон Рус [2] и Кенет Фалконър [3]. Теорията на фракталите е част от Теорията на хаоса. Има мнение, че след Теорията на относителността и Квантовата механика, Теорията на хаоса е третото най-важно достижение на науката на ХХ век. Все пак, методите на фракталния анализ не са така мощни и универсални, както е изглеждало в началото, но те са много полезни в случаи, когато други методи са трудно приложими, например за анализ на редове от данни с неравномерна стъпка.
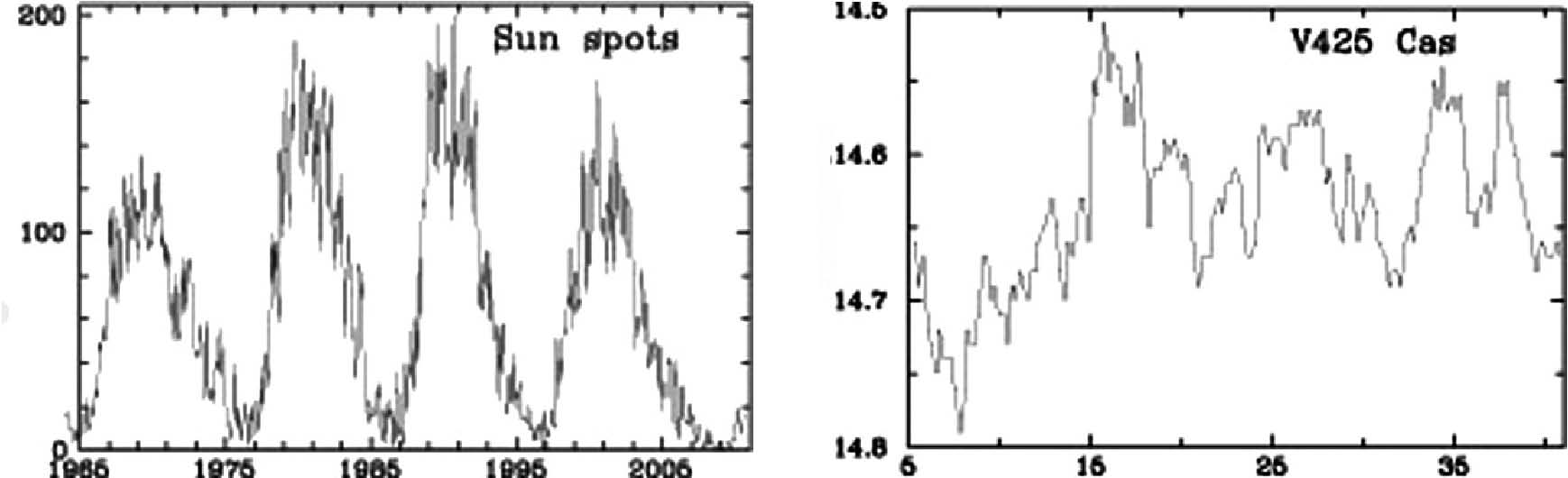
Фиг. 2. Примери за фрактали от тип начупени криви или редове от данни. Вляво – ходът на месечния брой слънчеви петна от 1965 до 2009 г. Вдясно – ходът на блясъка (в звездни величини) на катаклизмичната звезда V425 Cas при 40 минутен мониторинг [4].
Според Манделброт [1] фракталът е структура, която, на по-малки и още по-малки мащаби съдържа структури, подобни на нея, цялата. Има множество природни фрактали. Фигура 1 илюстрира фрактал от тип фрактелна повърхност. Всеки разрез на такава повърхност, представляващ начупена крива, има самоподобна назъбеност и попада в типа фрактелен профил. Като фрактален профил може да се разглежда и всеки ред от данни, например месечният брой слънчеви петна (фиг. 2, вляво) или бързите промени в блясъка на някои звезди (фиг. 2, вдясно).
Степента на фракталност на привидно хаотични природни структури се характеризира за изследователски цели чрез специалната величина фрактална размерност. Нейното въвеждане пък, се базира на наклона на т. нар. фрактална зависимост (фрактален плот).
2. Фрактални плотове на сложни криви линии в равнината
Бреговите линии и сухопътните граници на държавите са класически примери за фрактали от типа сложни криви в равнината.
По време на Втората световна война английският физик-теоретик, математик и пацифист Люис Фрай Ричардсън бил осенен от мисълта, че агресивността на една държава или империя расте с нарастването на нейната граница. Той възнамерявал да оцени вероятността за война между две съседни държави чрез дължината на общата им граница, но при набирането на данни срещнал сериозен проблем. В различни справочници дължините на границите на бреговите линни на държави като Англия, Белгия и Холандия се отличавали на 20-30%, а понякога и 2 пъти. Ричардсън решил сам да измери дължината на бреговата линия на Британия. Той взел географска карта и измерил дължината на бреговата линия, обхождайки я с минимално разтворен пергел. После той вземал все по-подробни карти и чрез същата стъпка получавал съответно по-дълги брегове. По-нататък Ричардсън установил същото и за бреговете и сухопътните граници на други държави.
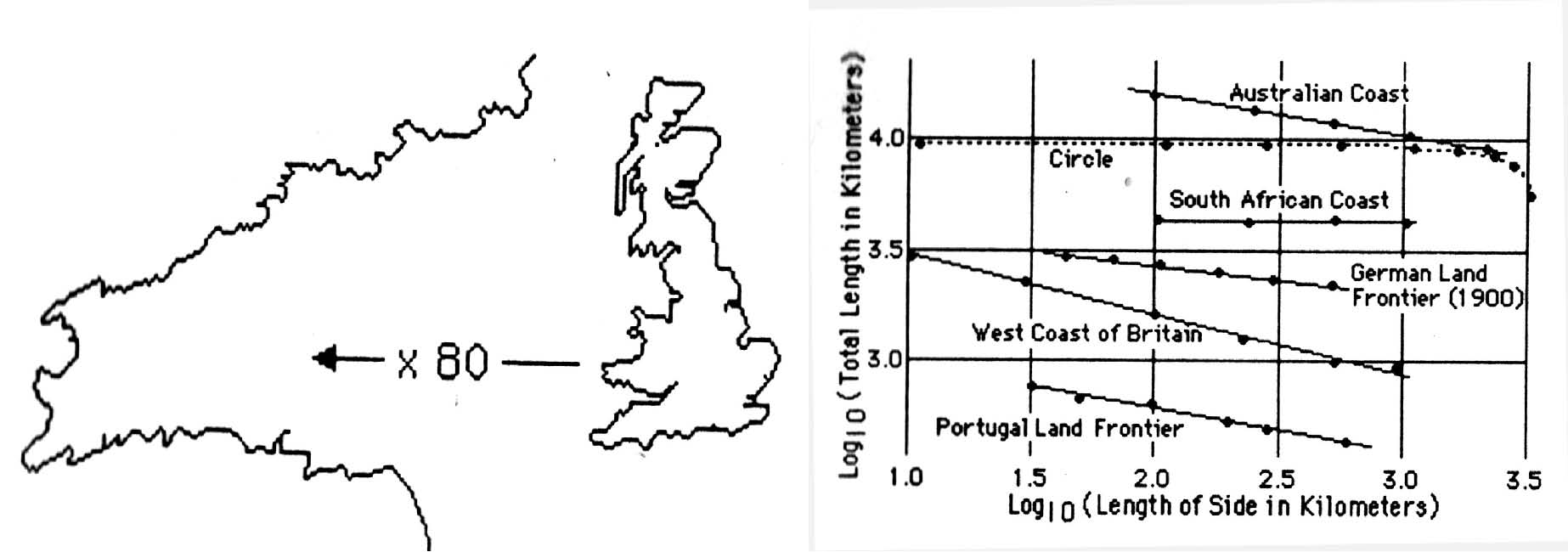
Фиг. 3. Вляво: Визуално представяне на самоподобността на назъбеността на британския бряг при 80-кратно увеличение [2]. Вдясно: Плотовете на Ричардсън в log-log координати [5], където западният бряг на Британия, като най-силно ерозиран, е с най-голям наклон.
Ясно е, че все по-подробните карти разкриват все повече детайли на бреговата линия (Фиг. 3, вляво) и тя излиза все по-дълга. Удивително е, че нарастването става с изпреварващ темп, по добре изразен степенен закон. Голямата заслуга на Ричардсон е, че той е съпоставил стъпката на измерване s и получената дължина S и намерил добре изразени линейни зависимости в логаритмични координати, съответстващи на степенни зависимости в линейни координати
(1) log S = а + b×log s или S ~ sb
След смъртта на Ричардсън през 1951 г. негови колеги събрали и публикували от негово име през 1961 г. [5] широко известните днес плотове (зависимости) на Ричардсън в log-log-координати (фиг. 3, вдясно). Техните наклони представят различните по ерозираност австралийски бряг, южно-африкански бряг, германска сухопътна граница през 1900 г., западен британски бряг и португалска сухопътна граница. Най-силно ерозиран и затова с най-голям наклон на плота (около -0.3) е западният британски бряг. Трябва да се отбележи специално, че такива плотове за „нормалните” геометрични фигури имат наклони 0. На фиг. 3, вдясно, това е показано за окръжност с дължина 10 000 км (пунктир).
И така, наклонът на плота на Ричардсън, т.е. правата линия (1) в log-log координати, характеризира назъбеността или ерозираността на бреговата линия По-стръмните плотове съответстват на поерозирани брегове. В този случай плотовете имат диапазони на линейност по абсцисата 1-2 порядъка. При големи стъпки, сравними с размера на обекта, плотът тръгва надолу и свършва, както при окръжността, вдясно. При малки стъпки, когато дребните детайли станат неизмерими или пренебрежими, плотовете следва да клонят към хоризонтали. Типично е, че плотовете на Ричардсон се отличават с малък разброс и значи, с много точно определяем наклон.
3. Математични фрактали и фрактална размерност на начупена крива
Математично-генерираните фрактали, онагледяват самоподобието и количественото характеризиране на фракталността чрез величината фрактална размерност. Такива обекти се „произвеждат” по два начина – чрез последователно намаляване или разделяне на единичен начален обект (фиг. 4, вляво; фиг. 5) или пък чрез последователно увеличаване или размножаване на единичен обект (фиг. 4, вдясно, фиг. 11). Първият начин е по-разпространен и по-нагледен.
3.1. „Нормални” отсечки, фигури и тела
Нека имаме начален обект с единичен размер в пространство с (топологична или евклидова) размерност D=1 (линия) или D=2 (равнина) или D=3 (тримерно пространство). Съответните прости единични обекти са, например, отсечка или квадрат или куб (фиг. 4, вляво, горе). Нека разделим всеки единичен обект във всички направления последователно 2, 3, ..., l пъти. Тогава за всяко l броят Nl на новите, по-малки самоподобни обекти, които покриват цялата му дължина или площ или обем на входния обект, е свързан с размерността D чрез формулите
- (2)
- Nl = lD или D = log Nl / log l. Тези равенства са изпълнени за всеки от трите редове картинки на фиг. 4, вляво и вдясно, както и за всички следващи, непоказани, случаи. При това D е цяло число, 1 или 2 или 3 и т.н., за всяко l. Приема се, че размерността D на тези прости обекти е и тяхна фрактална размерност. Фрактална размерност D на съществено по-сложни обекти, съдържащи самоподобни компоненти, която може да бъде нецяло число, се дефинира по аналогия с (2):
- (3)
- D = lim[ log N(e) / log (1/e) ], при е→0, Тук e е размерът на елементарната структура, а N(e) е броят на елементарните структури с размер е, покриващи целия обект.
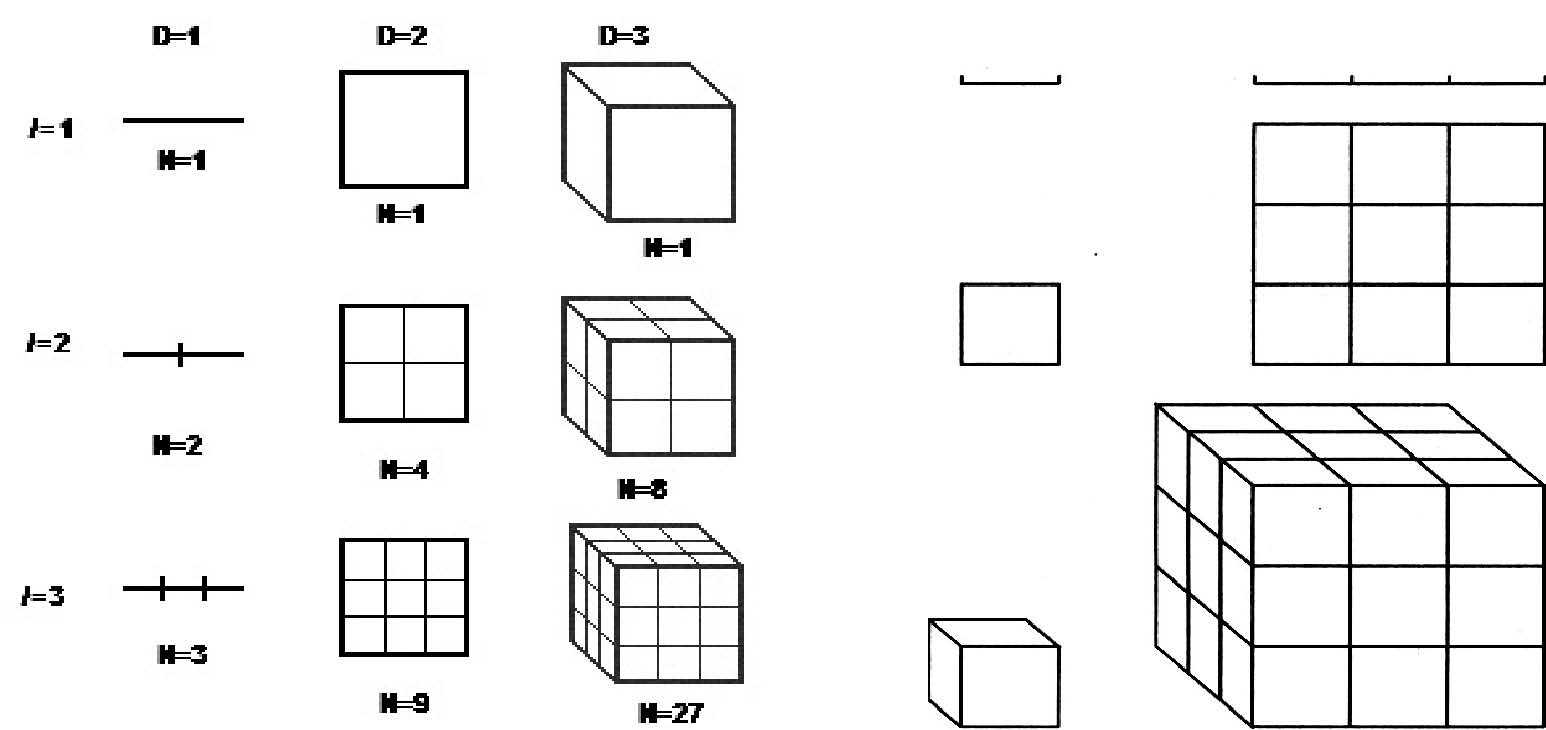
Фиг. 4. Топологична размерност D и фрактални вместимости N(l) = lD при „нормални” геометрични обекти. Вляво
– при последонателно раделяне на обекта; Вдясно – при последователно размножаване на обекта.
3.2. Начупени криви на Кох
Сред математичните обекти най-прости и най-близки до фракталите от тип начупена линия са криви-те на Хелге фон Кох, предложени през 1901 г. (фиг. 5). Всяка от тях се строи итеративно с делител l=3. При итерация n=0 входният обект е отсечка с единична (или произволна крайна) дължина. При всички математични фрактали при първата итерация (n=1) се задава «генераторът» на процеса. За кривата на Кох с триъгълници (фиг. 5, вляво) той се състои в следното: средната 1/3 част от отсечката се заменя с две такива отсечки, образуващи с отстранената средна част равностранен триъгълник. Дължината на получената начупена крива става 4/3. При втората итерация (n=2) средната 1/3 част от всяка от четирите отсечки се заменя с две отсечки, образуващи с отстранената средна част равностранен триъгълник. Дължината на получената начупена крива става (4/3)2 = 16/9 и т.н.
Забележително при кривата на Кох е, че с увеличаването на n броят на отсечките (4n) и дължината Sn = (4/3)n клонят към безкрайност, обаче за всяко n кривата заема само точките от една начупена линия в равнината с краища като на входната отсечка. Това е възможно понеже кривата на Кох излиза от първоначалното си едномерно пространство като част от права линия и се простира в двумерното пространство като част от равнина.
Нека приложим дефиниците за фрактален наклон по Ричардсън (1) и за фрактална размерност (2 и 3) към дължината но кривата на Кох с триъгълници за n>0. С намаляване на стъпката 3 пъти дължината нараства 4/3 пъти (фиг. 5, вляво). Следователно наклонът на плота на Ричардсън, b<0, е
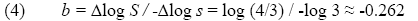
Същевременно спрямо всяка предишна итерация дължината на кривата става 4/3 и може де се запише
(5) 4n = (3n)D или D = log 4 / log 3 ≈1.262, т.е. D = 1– b.
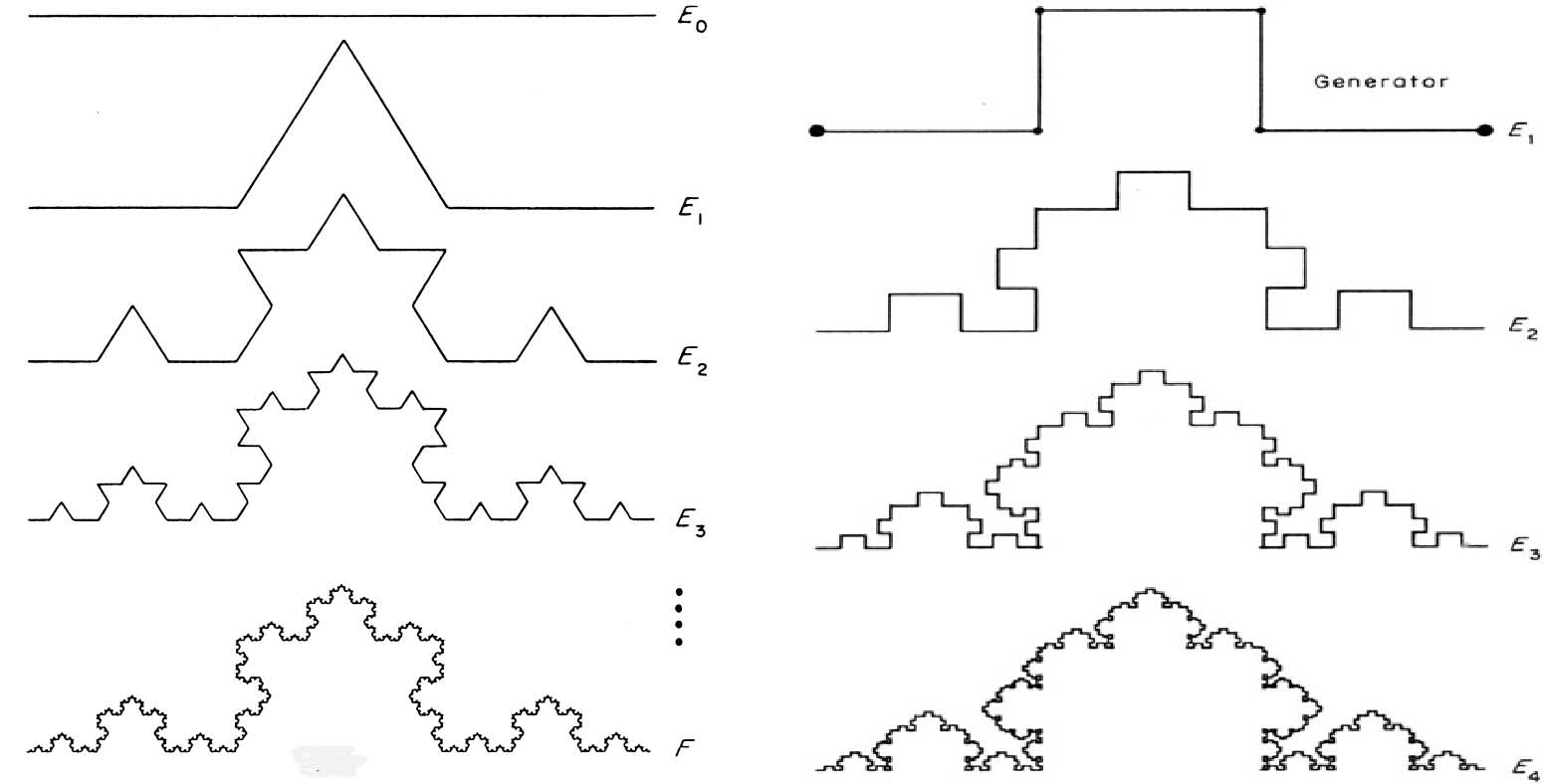
Фиг. 5. Фракталът «начупена крива на Кох». Влаво – с триъгълници, итерации n = 0,1,2,3, 5. Вдясно – с прававоъгълници, итерации 1.2.3.4 [3]. Кривите имат делител l=3, дължини S → ∞, наклони на плота на Ричардсън b равни на -0.262 и b =-0.465, както и фрактални размерности D =1 – b равни на 1.262 и 1.465.
Има и по-силно начупена крива на Кох, където отстранената средна третина на отсечката се заменя с трите страни на квадрат, построен над нея. Тогава за кривата на Кох с квадрати се получава Sn = (5/3)n , b=-0.465 и D =1.465. При кривата на Кох с квадрати върховете на квадратчета от съседни сегменти започват да съвпадат и нагледността пропада. Това се избягва при крива на Кох с правоъгълници (фиг. 5, вдясно [3]), която е «по-ниска» от кривата на Кох с квадрати.
Фракталната размерност на западния британски браяг е D ≈ 1.3. Максимална фрактална размерност на начупена крива в равнината, D =2, има брауновото движение.
3.3. Накъсани отсечки (прах) на Кантор
Друг широко известен математичен фрактал, който е „антипод” на кривата на Кох е прахът (или множеството) на Георг Кантор от 1883 г. В случая, показан на фиг. 6, вляво, входният обект е отсечка, делителят е пак 3, но отстранената вътрешна 1/3 част от всяка отсечка не се заменя с нищо. Така с увеличаване на n броят на отсечките расте като 2n и всички отсечки остават в рамките на първоначалната отсечка, но общата дължината на отсечките, Sn = (2/3)n, клони към нула.

Фиг. 6. Фракталът „прах (отсечки) на Кантор”. Вляво – с отстраняване на вътрешната 1/3 част от всяка отсечка, итерации 0-5, с b = 0.369 и D = 0.631. Вдясно -с отстраняване на вътрешната 1/5 част (горе) или вътрешната 1/2 част (долу) от всяка отсечка, итерации 0-4. В последния случай имаме b =0.5 и D =0.5
При праха на Кантор (на фиг. 6, вляво) за наклона на плота на Ричардсън, b>0, е в сила
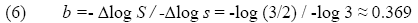
Същевременно спрямо всяка предна итерация дължината на кривата става 2/3 и може де се запише
(7) 2n = (3n)D или D=log 2/log 3 ≈0.631, т.е. пак D =1 – b.
На фиг. 6, вдясно, е представен „по-едър”, горе, и „по-ситен”, долу, прах на Кантор. В последния случай на всяка следваща итерация се отнема средната 1/2 част от всяка отсечка. Получава се Ln = (2/3)n , l=4, b = 0.5 и D = 0.5
Примерите, а и теорията, показват, че при начупени линии в равнина или пък при ерозирани отсечки в линия, фракталната размерност D и наклонът на плота на Ричардсън b са свързани с простата фундаментална формула
(8) D = 1 – b.
Има мнение, че природен аналог на праха на Кантор могат да бъдат пресечниците на пръстените на планетите (като отсечки) с радиални линии, изхождащи от центровете на планетитите и лежащи в равнините на пръстените [1].
3.4. Други класически математични фрактали – фигури и тела
На фиг. 7, вляво, е представен математичен фрактал от тип фигура в равнината – триъгълен килим (салфетка) на Вацлав Сиерпински от 1915 г. При него началният обект, при n=0, е триъгълник с площ 1, а линейният делител е l=2. При n=1 средната част на триъгълника – обърнат триъгълник със страна ½ от началната – се отстранява и не се отчита по-нататък като площ. Останалата площ е ¾ от началната, но в нея два пъти по-малкият по страна триъгълник се нанася 3 пъти. При n=2 с всеки от трите черни триъгълника се процедира както с първия, като дупките в средите не се отчитат по-нататък. Останалата

Фиг.7. Двумерни аналози на прака па Кантор. Вляво: Триъгълник на Сиерпински с D = 1.585, итерации 0, 1, 2 и 5. Вдясно: Квадрат на Сиерпински” с D = 1.893, итерация 3.
При n-тата итерация на триъгълника на Сиерпински останалата площ е Аn = (3/4)n . Тук с увеличаването на n броят на триъгълниците расте като 3n, всички триъгълници остават в рамките на началния триъгълник и аналогично на праха на Кантор площта A клони към 0.
На фиг. 7, вдясно, е показана третата итерация на квадратен килим на Сиерпински с площ An = (8/9)n. Килимите на Сиерпински са двумерни аналози на праха на Кантор, но в случая останалите след всяка итерация точки не са разпокъсани, а свързани. Те принадлежат на фигура, състояща се от мънички триъгълници или квадрати с дупки в средата. Аналогично на праха на Кантор, килимите на Сиерпински остават в първоначалното си (тук – двумерно) пространство.
С намаляването на стъпката от килимите на Сиерпински се отнемат части и площта клони към нула (b>0). За тях са приложими дефинициите за фрактален наклон (1) и фрактална размерност (2, 3) За триъгълника на Сиерпински, следва да се запише
(9) b= log (4/3) / log 2 = 0.415, 3n = (2n)D или D = log 3 / log 2 ≈ 1.585.
За квадрата на Сиерпински се се получава D = 1.893. При фракталните фигури в равнината простата основна формула за фракталната размерност е
(10) D = 2 – b.
Анологично на кривите на Кох с триъгълници или квадрати, могат да се разглеждат и характеризират фрактално начупени повърхности на Кох с тетраедри или кубове (фиг. 8). Техните площи клонят към безкрайност, защото те излизат от равнината и се развиват в пространството.
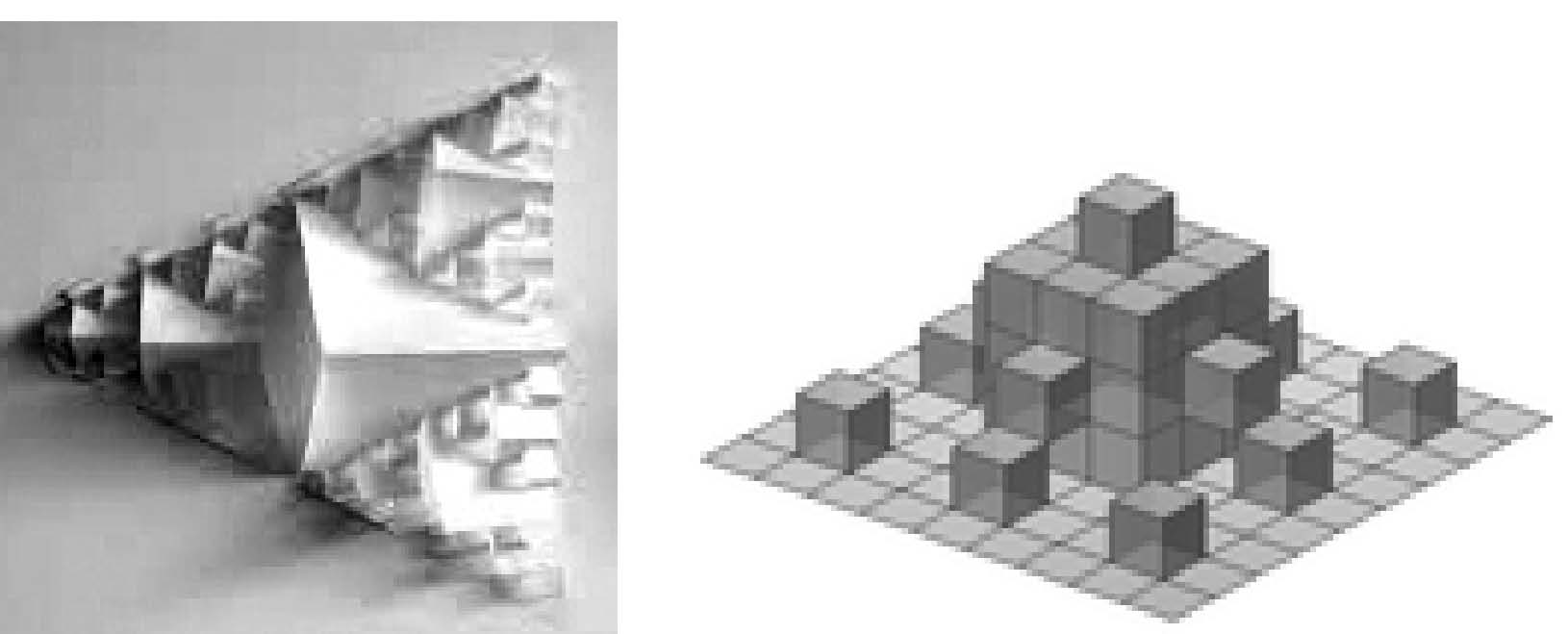
Фиг. 8. Вляво – непълна повърхност на Кох с тетраедри, итерация 4, където размножаването на тетраедрите върви само в равнината на първоначалния триъгълник. Вдясно – повърхност на Кох с кубове, итерация 2.
Също така могат да се разглеждат тетраедър на Сиерпински и куб на Сиерпински (известни и като “сюнгери на Менгер”), при които се отнема само централния тетраедър или куб. Външно те са „непрозрачни” и неотличими от тетраедър или куб, като „изяждането” става винаги отвътре. Тези тела се характеризират с обеми клонящи към 0 и съответни фрактални размерности D = 2.678 и D = 2.966.
При фракталните тела в пространството за фракталната размерност е в сила формулата
(11) D= 3 – b.
4. Фрактални размерности при плотовете площ – периметър
Зависимостта площ -периметър, в log-log координати, се използва често за фрактален анализ на формите на множества от сложни равнинни фигури като водосборни басейни на реки, острови, атмосферни облаци, облаци междузвезден газ, слънчеви фотосферни гранули и др. Методът е приложим и за анализ на фрактални повърхности, чрез фигурите, оградени от изолинии.
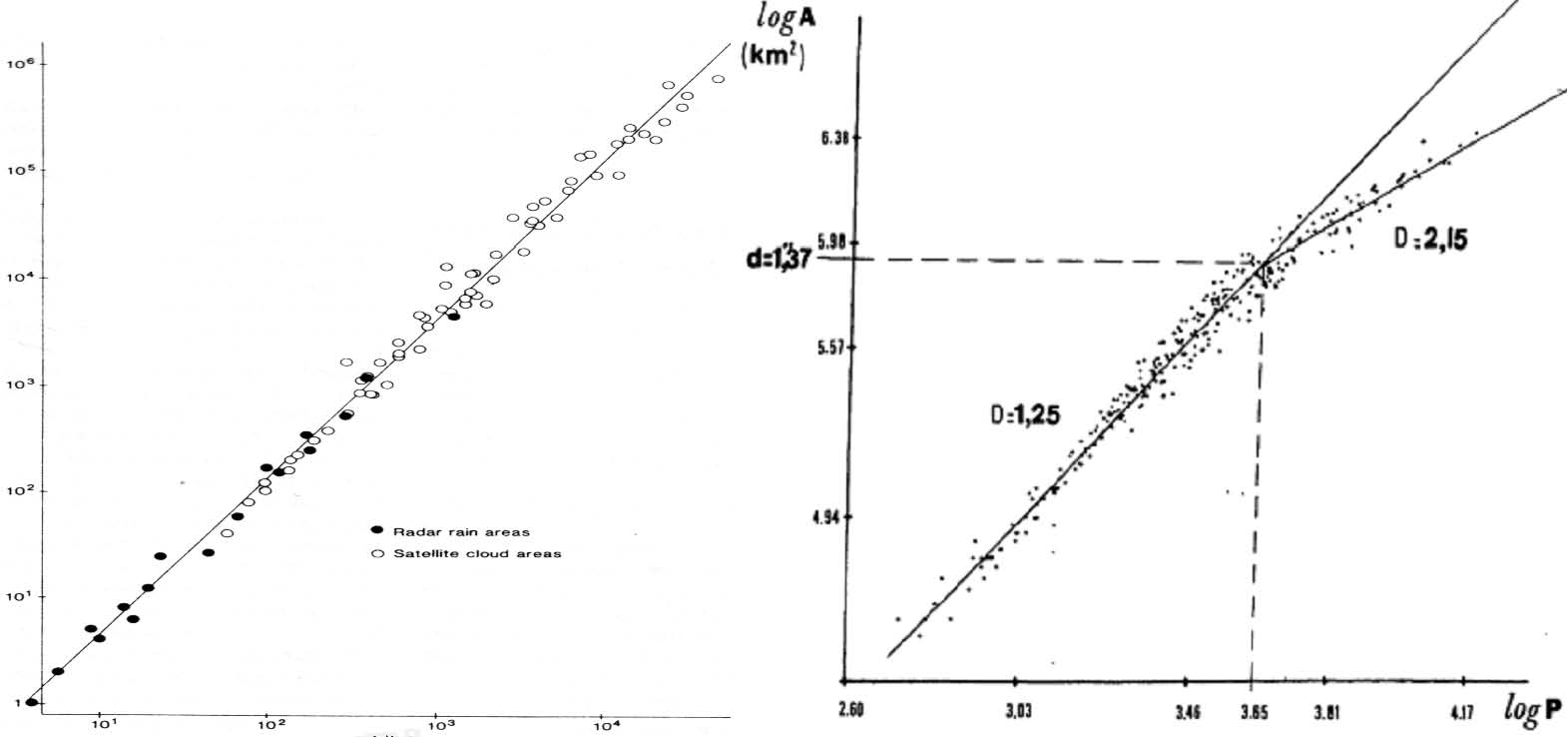
Фиг. 9. Класически примери за зависимости пeиметър (абсциса) – площ (ордината), в логаритмични координати. Вляво – за атмосферни валежни зони (по радарни занни, точки) и облачни зони (по спътникови снимки, кръгчета) с разери 1 – 1000 км по Лавджой [6] (D = 1.35). Вдясно – за слънчеви фотосферни гранули с размери 100 – 2000 км по Родие и Мюлер [9] (зависимостта е бифрактална, D= 1.25 и D =2.1
На фиг. 9, вляво, е представен основният резултат от пионерската работа на Лавджой от 1982 г. [6]. Той определя площите A и периметрите L на множество валежни зони (по радарни данни, точки) и облачни структури (по спътникови снимки, кръгчета), с площи от 1 до 1 200 000 кв. км. и намира зависимостта
(12) log L = а + b log A или L ~ Аb с b = 0.675. Правата линия в log-log координати индикира отсъствие на характерен размер на валежните и/или облачни зони в диапазон размери 3 (!) порядъка. Авторът е препоръчал да се направи подобно изследване за облачната структура на Юпитер, където диапазонът на размерите може да бъде 5 порядъка, а наклонът на зависимостта следва да бъде друг.
Вега и др. през 1996 г. [7] и установено наблюдателно от Вестфал и др. през 1999 г. [8]. През 1957 г Хак определя периметрите L и площите А на водосборните басейни на големите земни реки и получава в log-log координати b = 0.6 ([1], стр. 111).
Фракталността на слънчевата фотосферна гранулация е изследвана най-напред от Родие и Мюлер през 1987 г. [9], които определят площите и периметрите на гранули с размери 100 – 2000 км и строят зависимости от вида (12). Те намират две категории гранули, по-големи и по-малки от 975 км, даващи бифрактална зависимост с наклони: 0.625 и 1.075 (фиг. 9, вдясно). Авторите твърдят, че по-малките гранули имат турбулентен характер и поставят под съмнение съществуването на по големите, защото този коефициент на наклон теоретично не може да бъде по-голям от 1 (вж. по-долу).
Особено интересна е работата на Манделброт и др. от 1984 г. [10], където за анализ на фрактални повърхности (фрактури на стоманени детайли) се използва плотът периметър – площ. За целта фрактурата се покрива електролизно с манган, а след това се шлайфа фино. Сред „морето” на мангана се показват „острови” стомана. Картината се дигитализира и за островите се строи зависимостта периметър-площ. При това „островите с езера се игнорират, а островите с езера и острови в езерата се включват”. Резултатът за даден образец стомана е добре изразена права линия, подобна на фиг. 9, вляво, но в 2 порядъка размери. В крайна сметка е построена зависимост «фрактална рамерност – енергия, необходима за счупването». Така е създаден и калибриран обективен метод за определяне якостта на стоманата апостериорно, когато счупеното парче може да е негодно за стандартен анализ на якостта.
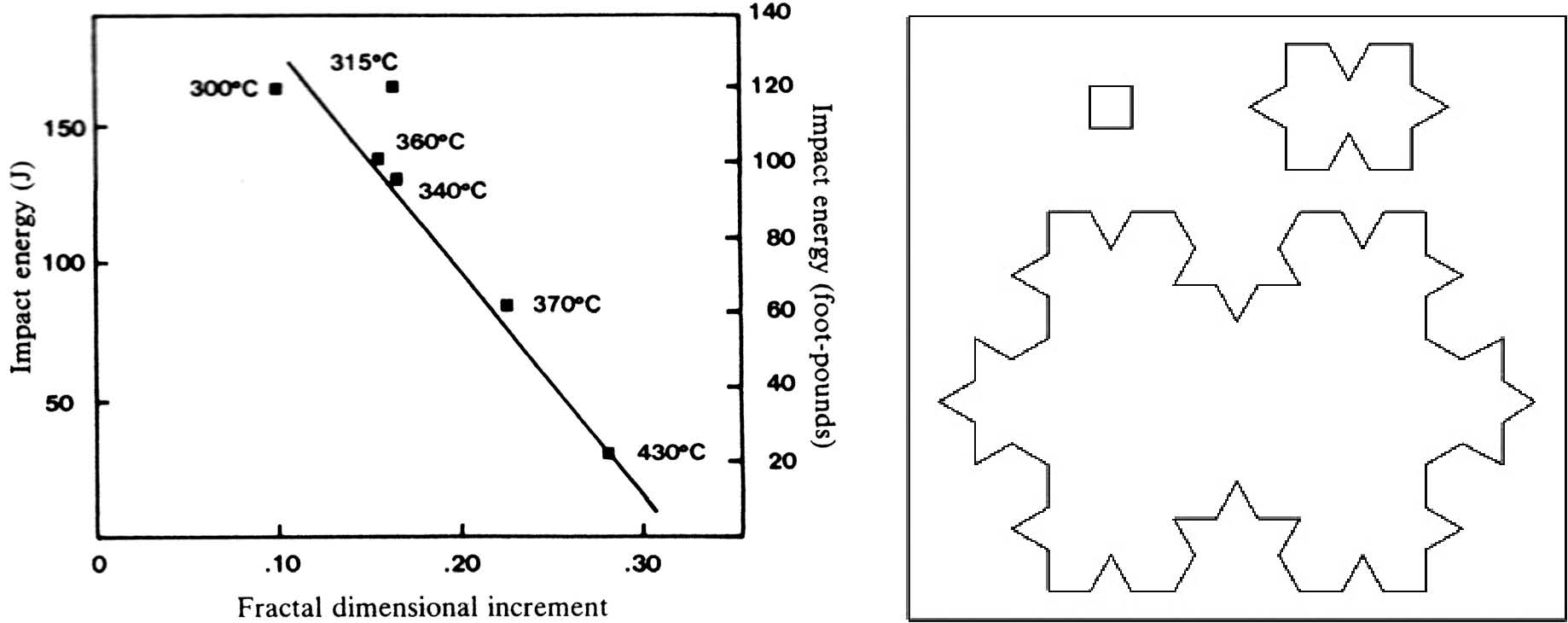
Фиг.10. Вляво: Приложение фракталната размерност, получена чрез плот периметър-площ, за оценяване на якостта на стоманата на вече счупен детайл по Манделброт и др., 1984 г., [10]. Вдясно: Фракталът «Назъбен облак,» специ-ално създаден тук за илюстрация на фракталност при отношението периметър-площ (итерации 0,1,2; с D =1.524).
За въвеждането на фрактална размерност на базата на отношението периметър-площ 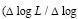 A1/2 ) и за разкриване на физическия смисъл на тази фракталност, ще си послужим пак с математични аналогии. Тъй като размерът е пропорционален на корен квадратен от площта, то на зависимостта log L = а + b × log A всички обикновени геометрични фигури се характеризират с b = 0.5, както следва. A1/2 ) и за разкриване на физическия смисъл на тази фракталност, ще си послужим пак с математични аналогии. Тъй като размерът е пропорционален на корен квадратен от площта, то на зависимостта log L = а + b × log A всички обикновени геометрични фигури се характеризират с b = 0.5, както следва.
За триъгълник със страна 1 имаме L = 3, A = 31/2/4 A1/2= 31/4/ 2, следователно
(13А) L = (6/31/4) A1/2 и log L = 0.5 log A + 0.659
За квадрат със страна 1 имаме L = 4, A = 1 A1/2 =1, следователно
(13В) L = 4 A1/2 log L = 0.5 log A + 0.602
За кръг с диаметър 1 имаме L = π, A = π/4 A1/2 = π1/2/2, следователно
(13С) L = 2 π1/2 A1/2 и log L = 0.5 log A + 0.549
На фиг. 11, вдясно, на плотове „площ – периметър”, в log-log координати, тези фигури (а и всички обикновени геометрични фигури) дават прави линии с наклон ½ и различно вертикално отместване. Една необикновена равнинна фигура, с фракталност на периметъра, следва да се характеризира със зависимост от вида
L ~ AD/2
(14) L ~(A1/2) D или и log L = D/2 log A + const, с D>1. Затова фракталният наклон b и фракталната резмерност D следва са свързани с равенствата
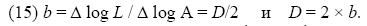
Изобщо, при плотове „периметър – площ” за равнинни фигура фракталната размерност е свързана с наклона на линията чрез простата фундаментална формула
(16) D = 2 ×b.
Следователно, оценките на фракталните размерности на примерите са следните: за облаците на Лавджой ≈1.35, при водосборните басейни ≈ 1.2, при слънчевата гранулаця ≈1.25, за слабата стомана на Манделброт ≈ 1.28.
Според старите интерпретации на отношението периметър-площ по-високият от ½ коефициент на log-log диаграмата свидетелства, че малките детайли (острови, облаци) са по-скоро закръглени, а големите стават все по-разтеглени и разкривени. Манделброт акцентира върху неправилността на тази интерпретация ([1], стр. 111) и пояснава, че дължините на периметрите, като начупени линии в равнината, могат да бъдат интирпритерани напълно в духа на плота на Ричардсън. С други думи, малките обекти имат къси периметри и там не могат да се вместят широк диапазон назъбености. Все по-големите обекти имат все по-дълги периметри. Те вместват все повече и с различни мащаби детайли и стават по-дълги с нарастващ темп спрямо нарастването на площта. Затова на log-log диаграмата се наблюдава права линия.
За да стане тази интерпретация очевидна, тук публикуваме специално създадена за случая равнинна фигура с фракталност на отношението периметър – площ b > ½. (фиг. 11, вляво). Да я наречем «Назъбен облак”. Началният обект (при n=0) е квадрат с площ А. Генераторът на фрактала (n=1) се състои в увеличаване на площта А на квадрата 9 пъти (т.е. размерът А1/2 = 3 пъти) и замяна на страните на квадрата с четири криви на Кох със същия номер итерация. Тези криви са две по две обърнати една срещу друга, така че площта на фигурата остава 9 пъти по-голяма отколкото при предната итерация. При всяка следващата итерация (случаят n=2 е показан) се прави същото. При това всеки път величината А1/2 нараства 3 пъти, а дължината на кривата на Кох, обхващаща площта, нараства 4/3 пъти. Следователно за първа итерация на фрактала Назъбен облак (с криви на Кох с триъгълници) имаме както в (13-16)
(17) 3D = 16/3, D = log (16/3) / log3 = 1.524 и b = 0.762. Аналогично може да се характеризира и фрактален назъбен облак с периметър, състоящ се от четворки криви на Кох с квадрати, за който се получава D = 1.727 и b = 0.863.
Наклоните на разгледаните тук фрактални зависимости са илюстрирани върху плота за слънчевата гранулярност, с наклон 0.575 (фиг. 11, вдясно). Прекъснатите прави долу вдясно, с наклони 1/2 съответстват на правилните фигури триъгълник, квадрат и кръг. Прекъснатите линии горе-вляво съответстват на назъбени облаци със квадрати и триъгълници, с наклони съответно 0.727 и 0.824. Облаците на Лавджой и водосборните басейни на Хак дават наклони съответно 0.675 и 0.6 Назъбените облаци с триъгълници и квадрати дават наклони 0.762 и 0.863.
5. Заключение
Тази статия е предизвикана частично от неотдавнашната кончина на забележителния учен и фактически създател на фракталния анализ – Беноа Манделброт (1924-2010). Тук са представени само най-основните понятия и зависимости при фракталния анализ на начупени криви в равнината.
Множество други подходи и методи могат да се намерят например в работите [1], [2] и [3]. Обширна информация има и в Интернет.
Литература
[1]. Mandelbrot B.B., 1982, The fractal Geometry of Nature, Freeman, New York
[2]. Russ J.C., 1994, Fractal Surfaces, Plenum Press, New York and London
[3]. Falconer K., 1997, Techniques in Fractal Geometry, John Willey & Sons
[4]. Tsvetkova S., Boeva S., 2009, Bulgarian Astronomical Journal, 12, 43-47
[5]. Richaardson L.F., 1961, General Systems Yearbook 6, 139-187
[6]. Lovejpy S., 1982, Science 216, 185-187
[7]. De Vega H.J., Sanchez N., Combes F., 1996, Nature 383, 56-58
[8]. Westpfahl D.J., Coleman P.H., Alexander J., Tongue T., 1999, Astrophys. J. 117, 368-380
[9]. Roudier Th, Muller R., 1987, Solar Physics 107, 11-26
[10]. Mandelbrot B.B., Passoja D.E., Paullay A.J., 1984, Nature 308, 721-722
|
|