Департамент Икономика,

Нов Български Университет

Резюме Изследването прави преглед в приложението на Модела за оценка на капиталовите активи (Capital Asset Pricing Model) при определянето на цената на собствения капитал за целите на оценяването на активи. Прегледът има приложен характер, като се следват насоките, дадени в Международните стандарти за оценяване на IVSC и МСФО 13 Определяне на справедлива стойност. Прилага се модификация на метода, базиран на Модела за оценка на капиталовите активи с нивото на систематичния странови риск. Решават се два бизнес казуса, които отразяват условията на българската действителност, която притежава спецификите, характерни за повечето развиващи се пазари, както и гледната точка на два вида инвеститори.

Ключови думи: Цена на собствения капитал, оценяване на активи, модифициран модел за оценка на капиталовите активи

JEL: G10, G12

Два международни стандарта препоръчват използването на Моделът за оценка на капиталовите активи (MOKA) за основен за определяне на цената на собствения капитал при прилагането на приходния подход за оценка на активи.  Според параграф 21 на Технически информационен документ 1 (ТИД 1), издаден от The International Valuation Standards Council (IVSС), МОКА може да бъде коригиран за странови риск и други специфични рискове. В техническия документ не се прави разграничение в приложението на МОКА по отношение на няколко важни особености – (1) нивото на интеграция на даден капиталов пазар (пълна или частична интегрираност или изцяло сегментиран); (2) развитието на капиталовия пазар (дали е периферен, развиващ се или развит); (3) степента на диверсифицируемост на инвеститора (пълна, частична или недиверсифициран инвеститор). Много често при практическото приложение на модела тези особености се пренебрегват. От гледна точка на хипотезите на МОКА това е правилно, защото по презумпция те не съществуват -  не се прави разграничение на пазарите по ниво на интегрираност или развитие на капиталовия пазар, допуска се, че инвеститорите са диверсифицирани.

МСФО 13 по подобен на ТИД 1 начин препоръчва използването на МОКА при определяне на дисконтовия процент за целите на дисконтирането на паричните потоци. Илюстративният материал на IFRS Foundation за МСФО 13 [2012] приема МОКА като модел за определяне на цената на собствения капитал, като се споменават и другите модели като Теорията за арбитражното оценяване APT, и трифакторният модел на Fama and French [1992]. Нещо повече, в примерите, които са послужили за илюстрация, се отчитат специфики като страновия риск, ефекта на размера на компанията, и други рискове.

На практика хипотезите на МОКА много рядко съвпадат с действителността, което не пречи на неговата популярност. Изследване на KPMG привежда безспорни доказателства за използването на модела за оценка на капиталовите активи, въпреки спецификите на модела, които изчерпателно са изяснени в литературата. Моделът е използван винаги от 82% от анкетираните, като останалите 18% го използват понякога. Оказва се, че  няма институция, която да не използва МОКА. Нещо повече, наличието на множество разновидности на МОКА, разработени специално за развиващите се пазари, дават измамно, според нас, чувство на комфорт и увереност в приложението на модела в оценяването на активи.

Резултатите от изследването на KPMG, както и препоръките на IVSC 2011 и МСФО 13, ни мотивират да обърнем сериозно внимание върху проблемите при използването на този модел за определяне на цената на собствения капитал от страна на оценители, консултанти, анализатори и мениджъри. Ние предлагаме някои решения, които биха били полезни като ги илюстрираме чрез споделянето на два бизнес казуса.

1. Модел за оценка на капиталовите активи: Допускания и практическо приложение

Финансовата теория е предоставила инструментариум за определяне на изискуемата норма на възвращаемост в лицето на Модела за оценка на капиталовите активи. Много често при неговото практическо приложение се ниглежират предположенията, върху които той се гради. Те могат да се разделят на две основни групи. В първата група (група А) са предположенията, които се отнасят както за САРМ, така и за модерната портфейлна теория. Това са базови предположения, върху които обикновено се градят всички анализи в областта на инвестициите и портфейла. Във втората група (група Б) са предположенията, специфични само за САРМ. Тези предположения са поставени, за да може моделът да функционира в него­вата цялост. Някои от предположенията са доста тежки и правят модела трудно приложим в съвременната икономика. Много често в реалния икономически живот тези предположения не са изпълнени.

Таблица 1. Предположения на Модела за оценка на капиталовите активи Пътев и Канарян [2008]

Ние няма да извеждаме самото уравнение на МОКА, а ще дадем само крайният и всеизвестен му вид – уравнение 1, върху който ще разсъждаваме. МОКА отразява икономическата логика на рационален инвеститор, който може да диверсифицира своето богатство на интегриран капиталов пазар, без да е изправен пред някакви пречки и бариери. Поради това, въз основа на постановките на Модерната портфейлна теория и допусканията от Таблица 1, очакваната доходност от даден актив ще зависи от очакваната пазарна рискова премия, коригирана с измеритела на систематичен риск – коефициента бета.

Моделът за оценка на капиталовите активи (МОКА) е приет от анализатори и консултанти въпреки многобройните изследвания оборващи неговата полза. Появяват се разработки, които предлагат нови ad-hoc модели за определяне на цената на собствения капитал. Sabal [2004] и Fuenzalida и Mongrut [2010] сравняват основните модели, които са предложени за определяне на цената на капитала на развиващите се пазари. Sabal [2004] класифицира моделите според техния произход – академични и практични. Fuenzalida и Mongrut [2010] групират моделите в три групи според вида на инвеститора. Те разглеждат седем модела за определяне на цената на собствения капитал от перспективата на глобален добре диверсифициран инвеститор, два модела в случая на несъвършено диверсифициран инвеститор и един метод за недиверсифициран инвеститор.

Въпреки че Sabal [2004] разглежда моделите от гледна академична и практическа гледна точка, той достига до извода, че важно значение за определянето на цената на капитала има степента на диверсификация на инвеститора. Той избира набор от модели  за определяне на цената на капитала и се фокусира върху техните характеристики. На тази основа, Sabal избира най-обещаващите модели за оценяване на реални активи на развиващите се пазари.

Fuenzalida и Mongrut критично разглеждат всеки един от популярните модели за определяне на цената на капитала и достигат до извода, че нито един от тях не притежава преимущество пред останалите модели, когато трябва да се определи цената на капитала за всички сектори в шест латиноамерикански пазара. Те откриват, че латиноамериканските пазари се превръщат в по-интегрирани към Световния пазар, с което размерът на цената на капитала става все по-малка, което е съвместимо с изследването на Stulz [1999].

Sabal и Fuenzalida и Mongrut критично разглеждат десет моделa за определяне на цената на собствения капитал: (1) класическият МОКА на Sharpe [1964]; (2) Глобален и международен МОКА, предложен от Solnik [1974a, 1974b, 1977]; (3) Модифициран международен МОКА на Sabal [2002]; (4) Модел на Goldman Sachs, предложен от Mariscal и Lee [1993]; (5) Йерархичен модел на Lassard [1996]; (6) D-CAPM модел на Estrada [2002]; (7) Модел на Damodaran [2002]; (8) Модел наGodfrey и Espinosa [1996]; (9) Модел на Estrada [2000, 2001]; (10) ICCRC модел на Erb, Harvey и Viskanta [1995, 1995]. Изводите, до които те достигат не принасят категоричен довод в полза на една или друга разновидност на модела. Всяко предложение има своите предимства и недостатъци. Всеки инвеститор, анализатор, консултант трябва да обоснове избора на своя модел.

Моделът изисква използването на очаквана пазарна рискова премия, но на практика се използва историческа такава. Изследванията показват, че с намаляване на историческия период на изчисляване размерът, премията намалява. Причините за намаляващат арискова премия се свързват с развитието на капиталовите пазари, тяхната интеграция, редуцирането на транзакционните разходи, увеличаване на обемите на търговия.Това увеличава ликвидността и намалява риска. Тази особеност е характерна за висички развити пазари, но не и за развиващите се пазараи, още повече за периферните.

Изчисляването на собствена рискова премия за развиващ се пазар, например българския, e съпроводено с редица трудности, които изискват определени усилия и условни допускания, за да се преодолеят. Това от своя страна би довело до условен резултат, който едва ли ще бъде задоволителен, предвид усилията, които са вложени. Историята на българския фондов пазар е едва от 15 години, което е много малък период за извеждане на историческа рискова премия, а от друга страна не цялата икономика е представена на фондовата борса, за да може да направим правилните изводи и прецизно да приложим изчислената премия.

Въпреки условностите, които споменахме по-горе, Павлов (2015) търси и намира правдоподобно обяснение за величи¬ната на рисковата премия на акциите, чрез моделиране на водещи поведенчески кон¬цепции в условията на българския капиталов пазар. Той извежда справедливата рискова премия на акциите, посредством базов неокласи¬чески равновесен модел, основан на потреблението. На тази основа е приложен поведенчески модел, базиран на две широко известни специфики на човешкото поведение в условия¬та на риск и несигурност – склонността към избягване на загубите и тясното рам¬киране. Реалната рискова премия на българския фондов пазар за периода 2000 – 2014 г. е 11.72%.

Алтернатива на предложения от Павлов метод е използването на данни за пазарна рискова премия на еталонен пазар, например Германия или САЩ, за нуждите на определянето на цената на собствения капитал, след което да се изчисли изискуемата норма на доходност и в последствие да се приспособи към странови риск, липса на ликвидност, миноритарно участие.

Изследването на KPMG, което цитирахме по-горе, показва, че Bloomberg, Reuters и Capital IQ са основните източници на информация, когато става въпрос за рискова премия или бета коефициенти. Достъпът до тях е платен, но изследователският отдел на Credit Suisse изготвя и публикува на своя сайт [1] годишник с доходностите на на основните пазари (27 на брой, вкл. и регионални) - Credit Suisse Global Investment Returns Yearbook. Именно той би могъл да се използва като източник на данни за пазарна рискова премия.

От уравнение 1 е видно, че от коефициента бета зависи каква част от пазарната рискова премия ще изисква инвеститор от даден актив. Ако , инвеститорът в i –тия актив ще трябва да получи доходност по-висока от пазарната рискова премия. При  рисковата премия за отделния актив следва да бъде по-ниска от пазарната. При  инвеститорът ще получи рискова премия равна на рисковата премия за пазара. Следователно важността на коефициента бета е не по-малка от тази на рисковата премия. Поради това е необходимо да се обърне внимание на начините на нейното изчисляване и да изведем правила за определяне и приложение на бета коефициент:

Регресионният анализ е най-използваният метод за изчисляване на бета коефициента. Трябва да подчертаем, че съществуват други иконометрични методи, които изчисляват по прецизно коефициента бета, тъй като отчитат динамичната природа на риска на финансовите инструменти. Тъй като те са по-сложни и не толкова приложими в практиката, те не са обект на разглеждане.

Идеята е индексът да представя пазарния портфейл от рискови активи. За редица развити пазари има възможности за избор. Например за американските акции това е индекса S&P 500, но широкият индекс NYSE Composite също е използван, макар и не от толкова голям брой инвеститори. За Германия това е DAX, Франция CAC40, но когато се правят анализи на ниво ЕС, то не рядко се използва по-широкия и представителен индекс Stoxx Europe 600 или MSCI Europe.

Най-честият избор е използването на месечни данни за период от 5 години, което представлява извадка от най-последните 60 наблюдения за доходността на акцията и пазарния индекс. При седмични честота се прилага 3 годишен прозорец от данни. По подразбиране Bloomberg използва прозорец от данни за две години от седмични наблюдения. Методологията на Bloomberg е подходяща за прилагане на развиващи се пазари, тъй като използва по-скорошни данни, за пазари със сравнително кратка история и бързо развитие. Изследването на KPMG установява, че продължителността на периода, която е се използва в Австралия е между 2 до 5 години. Близо 50% от анкетираните използват 5 годишни данни, като 55% прилагат месечни стойности.

Изследване на Blume [1971] показва, че стойността на бета коефициента клони средно към 1, когато се прогнозира риска. Следователно е препоръчително да се използва уравнението на Blume [1971] за приспособяване към дългосрочната средна стойност 1, т.е. уравнение 2.

(2) ,

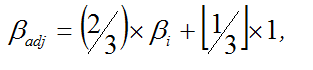Където:

 - приспособена бета към 1;

 - бета коефициент, получен чрез регресионния анализ, т.е. сурова бета.

Hamada [1972] предлага уравнение, което цели да се раздели финансовия риск от бизнес риска на фирма, която използва заемен капитал, т.е. ефекта на финансовия лост, за да увеличи стойността си. Уравнението съчетава теоремата Модилиани-Милър с МОКА и се използва, за да се определи лостовата бета, а чрез това, оптималната структура на капитала на фирмите. Уравнението на Хамада помага да се изведе лостовата бета (levered beta), т.е. бета коефициента на фирма, която се финансира с дълг и собствен капитал, от безлостовата бета, т.е. бета коефициента на фирма, която не се финансира с дълг, а само със собствен капитал. По този начин става възможно две фирми с еднакъв бизнес риск, но с различен финансов риск, да бъдат сравними за нуждите на бизнес оценяването (Уравнение 3).

За целите на сравнителния анализ трябва да имаме предвид, че бета коефициентът, изчислен чрез регресионния анализ, т.е. суровата бета, е лостова, ако фирмата финансира дейността си с дългов капитал. Следователно след като тя е приспособена към 1, то бета коефициентът трябва да се коригира с ефекта на лоста, за да остане само чистия бизнес риск. Накратко трябва да се изчисли безлостовата бета чрез уравнение 3’.

2. Приложен бизнес казуси: Цена на собствения капитал на различни видове инвеститори

Ние ще споделим два бзинес казуса, които успяхме да решим като приложихме описаната методология на Модела за оценка на капиталови активи. При тяхното решаване отчетохме особеностите, които описахме.  Ние разглеждаме два вида инвеститори – локален и глобален. За всеки един приложихме различна методология.

Локален Модел за оценка на капиталовите активи. Този метод е подходящ за определяне на изискуемата норма на възвращаемост при следните условия: (1) инвеститорът е локален (местен) на дадената държава, (2) той е напълно или частично диверсифициран, (3) пазарът не е интегриран към Глобалния финансов пазар.

Български рисков фонд иска да придобие дял във В фарма АД [2]. Дружеството е непублично, но с дългогодишна история и иновативни разработки. Фондът желае да придобие пакет от акции в дружеството. За определяне на справедливата стойност на компанията трябва да се изчисли нормата на дисконтиране. Тъй като В фарма АД използва дългово финансиране, макар и незначително, то дисконтовият процент ще бъде WACC.

Цената на собствения капитал се определя като се използва Софарма АД за аналог. Прилага се Моделът за оценка на капиталовите активи, чрез приспособяване на коефициента бета към 1 и финансовия лост на В фарма АД, чрез Софарма АД.

Изчисляването на безлостовата бета на Софарма АД става чрез уравнение 2. За целта се пъво се определя лостовата бета чрез регресионно уравнение. ИндексътSOFIX се използва за фактор, като на нализ се подлагат седмични стойности на доходността за период от 3 години [3].

Съотношението „Дълг/Собствен капитал“ се определя като се използват последно публикуваните консолидирани отчети към датата на анализа, т.е. 30.06.2015 г. Пазарната капитализация на дружеството се изчиалява с данните за наличните акции в обращение към 18.12.2015 г., както и среднопретеглената цена от борсовата сесия към 18.12.2015 г. Съотношението е изчислено като е използвана счетоводната стойност на дълга.

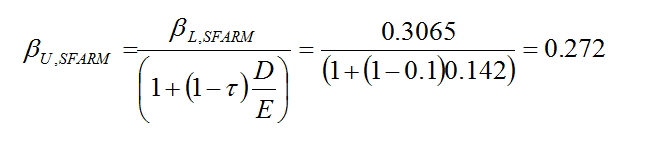
Стойността на съотношението Дълг/Собствен капитал на В фарма АД е много ниска едва 0.00257. Това се дължи на факта, че дружеството има много малък заемен капитал в размер на 9 000 лева, а счетоводната стойност на собствения капитал е 3 499 000 лева [4]. Данните са към 31.12.2014 г, тъй като източник на информация е Търговския регистър. Съотношението е изчислено чрез счетоводните данни. Оттук лостовата бета на В фарма АД е почти колкото безлостовата, т.е. 0.272

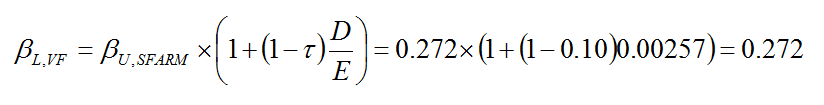
След приспособяване на лостовата бета на В фарма АД към 1 я заместваме в уравнението за изчисляване на цена на капитала.

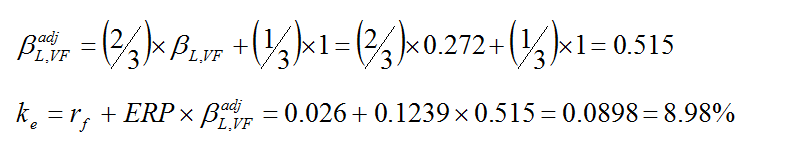
В горното уравнение са използвани данните за реална рискова премия, изчислена от Павлов [2015], която е превърната в номинална чрез използване на очакванията за инфлация на МВФ [5] (0.6%). Доходността на 10 годишните ДЦК на България към 18.12.2015 г. е 2.60% [6].

Глобален Модел за оценка на капиаловите активи, приспособен с нивото на систематичния странови риск. Този метод е подходящ за определяне на изискуемата норма на възвращаемост на чуждестранни напълно или частично диверсифицирани инвеститори, които инвестират във финансови активи или бизнес проекти в дадена страна.

Европейски рисков фонд иска да придобие дял във В фарма АД [7]. Дружеството е непублично, но с дългогодишна история и иновативни разработки. Фондът желае да придобие пакет от акции в дружеството. За определяне на справедливата стойност на компанията трябва да се изчисли нормата на дисконтиране. Тъй като В фарма АД използва дългово финансиране, макар и незначително, то дисконтовият процент ще бъде WACC. Фондът е заложил промяна във финансовото управление и се стреми към целеви дял на собствения капитал в капиталовата структура от 75%, докато делът на дълговия капитал да бъде 25%.

Цена на собствения капитал: МОКА с коригиращ коефициент за странови риск. Първо изчисляваме коефициента бета за сектора Фармация и Биотехнологии за Европа (Stoxx Pharm&Bio) спрямо широкия индекс Stoxx 600 Europe със седмични данни за последните 3 години [8]. Стойността на бета коефициента е 0.64, която се приспособява към 1.

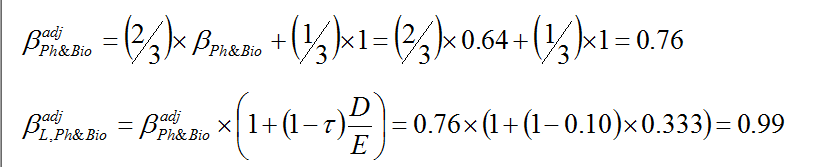
След приспособяване на секторната бета към целевия финансов лост я заместваме в уравнението за изчисляване на цена на собствения капитал. То се базира на МОКА, което приспособяваме към страновия риск. Използваме реалната пазарна рискова премия за Европа спрямо облигациите, изчислена за периода 1900-2014 г., от 3.30% [9]. Нея я привеждаме в номинална стойност, като използваме прогнозата на МВФ за инфлацията в Развита Европа за 2014 г. от 1.60% [10]. Оттук номиналната рискова премия се получава ERPE = 4.95%=(1+0.330)х(1+0.0160). Безрисковата доходност приемаме, че е равна на 3.428%, т.е. тази на 10 годишните ДЦК на България. Коригиращият коефициент за странови риск е изчислен като са използвани данни за Германия и България [11].

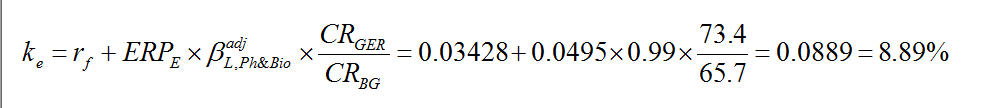
Трябва да уточним, че направихме допускане по отношение на коефициента бета на сектора „Фармация и Биотехнологии”. То е свързано с факта, че регресионната бета е безлостова. Ние сторихме това, тъй като нямаме информация какво е съотношението Дълг/Собствен капитал на секторния индекс, за да го използваме и изчислим безлостовата бета.

3. Заключение

В статията се прави критичен прглед на приложението на Модела за оценка на капиталовите активи при оценяване на активи. Извеждат се някои проблеми и се предлагат решения. Разгледани бяха два бизнес казуса, свързани с определянето на изискуемата норма на възвръщаемост от страна на два типа инвеститори. При решаването им е застъпено мнението, че трябва да се отчита спецификата на възложителя, т.е. какъв тип инвеститор е той. При локален инвеститор, който оперира на пазар, който не е интегриран към глобалния финансов пазар и не е диверсифициран, то следва да се използва класическия Модел за оценка на капиталовите активи. В случай, че възложителят е чуждестранен инвеститор и е напълно или частично диверсифициран, то следва да се приложи Глобалния Модел за оценка на капиталовите активи.

4. Литература

1.    Павлов, Цв. Приложение на поведенческите финанси при моделиране на българската рискова премия на акциите // Бизнес управление, брой 2, 2015г, стр. 96-130

2.    Пътев, Пл. и Н. Канарян, Управление на портфейла, АБАГР 2008.

3.    Blume, Marshall. 1971. “ On the Assessment of Risk. ” Journal of Finance . Vol. 26, No. 1: 1 – 10.

4.    Damodaran, A. Estimating Equity Risk Premiums New York: NY University, Stern School of Business Working paper, 2002

5.    Erb, C., C. Harvey, and T. Viskanta, Political Risk, Financial Risk and Economic Risk. Financial Analysts Journal, 1996, 52, pp. 28-46;

6.    Erb, C., C.R. Harvey and T. Viskanta, Country Risk and Global Equity Selection, Journal of Portfolio Management, 1995, 21, pp. 74-83.

7.    Estrada, J. Discount Rates in Emerging Markets: Four Models and An Application, Journal of Applied Corporate Finance, 19, 2000, pp. 72-77;

8.    Estrada, J. Systematic Risk in Emerging Markets: The D-CAPM. Emerging Markets Review, 2002, 3(4), pp. 365-379

9.    Estrada, J. The Cost of Equity in Emerging Markets: A Downside Risk Approach (II). Emerging Markets Quarterly, Spring 2001, pp. 63-72.

10. Fuenzalida, D., Mongrut, S. Estimation of discount rates in Latin America: empirical evidence and challenges. Journal of Economics, Finance and Administrative Sciences, 2010, Vol. 15, Issue 28, pp. 7–43

11. Godfrey, S., and R. Espinosa, A Practical Approach to Calculating Costs of Equity for Investments in Emerging Markets. Journal of Applied Corporate Finance, 1996, 9, 3, pp. 80-89.

12. Hamada, R.S. (1972) “The Effect of the Firm's Capital Structure on the Systematic Risk of Common Stocks,” The Journal of Finance, 27(2):435-452

13. International Valuation Standards, 2011, IVSC.

14. Illustrative examples to accompany IFRS 13 Fair Value Measurement Unquoted equity instruments within the scope of IFRS 9 Financial Instruments, December 2012, IFRS Foundation.

15. Lessard, D. Incorporating country risk in the valuation of offshore projects. Journal of Applied Corporate Finance, 1996, 9, pp. 52-63.

16. Mariscal, J.P. and R. Lee, The Valuation of Mexican Stocks, June, 1993

17. Sabal, J. Financial Decisions in Emerging Markets. Oxford University Press.2002

18. Sabal, J. The Discount Rate in Emerging Markets: A Guide, Journal of Applied Corporate Finance, 2004, 16(2-3), pp. 155-166.

19. Sharpe, W. F., Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk, Journal of Finance, 1964, 19, pp. 425-442

20. Solnik, Bruno, An equilibrium model of the international capital market, Journal of Economic Theory, 1974a, 8, pp. 500-524;

21. Solnik, Bruno, The international pricing of risk: An empirical investigation of the world capital market structure, Journal of Finance, 1974b, 29, pp. 48-54;

22. Solnik, Bruno, Testing international asset pricing: Some pessimistic views, Journal of Finance, 1977, 32, pp. 503-511.

23. Stulz, R. M. Globalization of equity markets and the cost of capital. NBER Working Paper No. 7021, 1999

24. Valuation Practices Survey 2013, KPMG, Corporate Finance, 2013, www.kpmg.com.au, p.11

25. World Economic Outlook: Adjusting to Lower Commodity Prices, October 2015, IMF, p. 32

26. World Economic Outlook: Transitions and Tensions, October 2013, IMF, р. 59

_________________________